Y=x^2-2x-15 \\ y=2x+6 Which of the following could be the y-coordinate of a point of intersection of the graphs of the two equations above in the xy-plane? A) -3 B) 5 C) 7 D) 20…

Question

`y=x^2-2x-15 \\ y=2x+6`

Which of the following could be the y-coordinate of a point of intersection of the graphs of the two equations above in the xy-plane?

A) -3
B) 5
C) 7
D) 20

Answer 1

• D) 20

Explanation:

Given functions

• y = x^2 - 2x - 15
• y = 2x + 6

Intersection is when the function have common points

• x^2 - 2x - 15 = 2x + 6
• x^2 - 4x - 21 = 0
• x^2 - 4x + 4 - 25 =0
• (x - 2)^2 = 25
• x - 2 = 5 ⇒ x = 7
• x - 2 = -5 ⇒ x = -3

y-coordinates are

• y = 2*7 + 6 = 20
• y = -3*7 + 6 = -15

Correct answer option is D) 20

Answer 2

`\huge\boxed{\text{(D) 20}}`

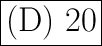
Explanation:

Our first goal is here to try and find the values of x that these equations meet at. We can then plug in the x-values into one of the equations (since their x values will be the same) and find the corresponding y value.

To find the x value that satisfies both equations, we can set both expressions equal to each other.

`x^2 - 2x - 15 = 2x+6`

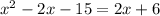
We can now solve for x.

Subtract 2x from both sides:

• 
  `x^2-4x-15=6`

Subtract 6 from both sides:

• 
  `x^2-4x-21`

We now have a polynomial in the form
`ax^2 + bx + c` ! We can factor this by finding two numbers that:

(A) When multiplied, get us
`c` (-21)

(B) When added together, get us
`b` (-4)

We know that
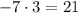`-7 \cdot 3 = 21` and
`-7 + 3 = -4`.

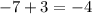Therefore our factorization is
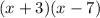`(x+3)(x-7)`, so the points at which these functions meet are -3 and 7.

We can now plug both of these values into one of the equations to find it's y value. Let's use
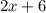`2x+6` (easier to work with).

-3:

`2(-3) +6\\\\-6+6=0`

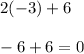
7:

`2(7)+6\\\\14+6\\\\20`

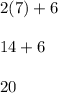
Since 0 isn't an option on the list, that means that (D) 20 would be a point of intersection of the two graphs.

Hope this helped!