Question

If a rectangle is altered by increasing its length by 20 percent and its width by 10 percent, its area increases by a percent. What is the value of a?

A) 25
B) 28
C) 30
D) 32

Answer 1

D) 32

Explanation:

`\textsf {The original equation would be :}`

`\implies \mathsf {area = length * width}`

`\textsf {Now, length has been increased by 20 percent and} \\\textsf {width has been increased by 10 percent.}`

`\textsf {Hence, new length and width will be :}`

`\implies \textsf {new length = length + 0.2(length) = 1.2(length)}`

`\implies \textsf {new width = width + 0.1(width) = 1.1(width)}`

`\textsf {Now the new area will be :}`

`\implies \mathsf {area' = 1.2(length) * 1.1(width)}`

`\implies \mathsf {area' = 1.32 * length * width}`

`\textsf {Now finding the percent change in area, 'a' :}`

`\implies \mathsf {a = (1.32 * length * width - 1 * length * width)/(1 * length * width)}`

`\implies \textsf {a = 0.32 = 32 percent}`

The correct option is D) 32 .

Answer 2

D

Explanation:

Recall that the area of a rectangle is given by the formula:

`A=\ell w`

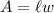
Where l is the the length and w is the width.

If we increase our length by 20%, this means that we add 20% or 0.2 of our old length to our old length. So, our new length will be:

`\ell_{\text{new}}=\ell + 0.2\ell = 1.2\ell`

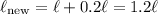
Similarly, if we increase our width by 10%, this means that we add 10% or 0.1 of our old width to our old width. So, our new width is:

`w_{\text{new}}=0.1w+w = 1.1w`

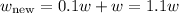
Therefore, our new area will be:

`A_{\text{new}}=(\ell_{\text{new}})\left(w_{\text{new}}\right)`

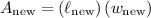
By substituting:

`A_{\text{new}}=\left(1.2\ell\right)\left(1.1w\right)`

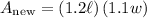
Multiply:

`\displaystyle A_{\text{new}}=1.32\ell w`

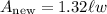
Recall that the old area is given by:

`\displaystyle A_{\text{old}} = \ell w`

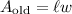
So, our area increased by a factor of 1.32. In other words, our area increased by 0.32 or 32%.

Therefore, our answer is D.