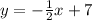Question

Line p is represented by the equation 2x-y=-5. If line r passes through the point (6,4) and is perpendicular to line p, what is the equation of line r?

Answer 1

`y = -(1)/(2)x + 7`

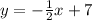
Explanation:

Given

`2x - y = 5`

`Point = (6,4)`

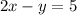
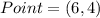
Required

Determine the equation of perpendicular line, r

First we need to determine the slope of the given equation

`2x - y = 5`

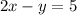
Make y the subject:

`y = 2x - 5`

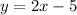
The general form of an equation is:

`y = mx + b`

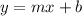
Where:

`m = slope`

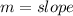
By comparison;

`m = 2`

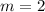
Since both lines are perpendicular:

We have:

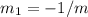`m_1 = -1/m` to calculate the slope of the perpendicular line

`m_1 = -(1)/(2)`

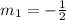
Equation of the line can be solved using:

`y - y_1 = m(x - x_1)`

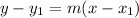
Where

`(x_1,y_1) = (6,4)`

`m = m_1 = -(1)/(2)`

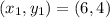
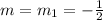
So: the equation becomes

`y - 4 = -(1)/(2)(x - 6)`

`y - 4 = -(1)/(2)x + 3`

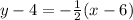
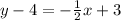
Solve for y

`y = -(1)/(2)x + 3 + 4`

`y = -(1)/(2)x + 7`

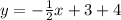
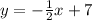
Hence:

The required equation is

`y = -(1)/(2)x + 7`