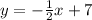Answer:
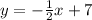
Explanation:
Given
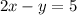
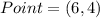
Required
Determine the equation of perpendicular line, r
First we need to determine the slope of the given equation
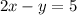
Make y the subject:
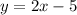
The general form of an equation is:

Where:
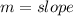
By comparison;
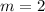
Since both lines are perpendicular:
We have:
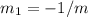 to calculate the slope of the perpendicular line
to calculate the slope of the perpendicular line
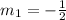
Equation of the line can be solved using:

Where
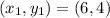
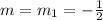
So: the equation becomes
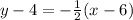

Solve for y
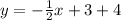
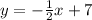
Hence:
The required equation is