Answer:
The equation of the line of reflection is
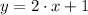 .
.
Explanation:
After looking carefullt the figure, we notice that line of reflection passes through B and midpoints in line segments AA' and CC'. If we know that
 ,
,
 ,
,
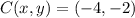 and
and
 , the midpoints of each line segment is:
, the midpoints of each line segment is:
Line segment AA'
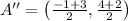
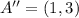
Line segment CC'
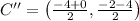

From Analytical Geometry we know that any linear function can be found by knowing two distinct points. The standard form of the linear function is represented by:
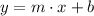
Where:
 - Independent variable, dimensionless.
- Independent variable, dimensionless.
 - Dependent variable, dimensionless.
- Dependent variable, dimensionless.
 - Slope, dimensionless.
- Slope, dimensionless.
 - y-Intercept, dimensionless.
- y-Intercept, dimensionless.
If we replace all variables with the components of the midpoints (
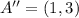 ,
,
 ), then we get a system of two linear equations:
), then we get a system of two linear equations:
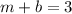 (Eq. 1)
(Eq. 1)
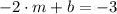 (Eq. 2)
(Eq. 2)
Lastly, we proceed to solve the system algebraically:
In (Eq. 1):
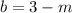
(Eq. 1) in (Eq. 2):
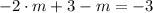

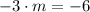
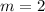
By (Eq. 1):
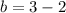
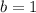
The equation of the line of reflection is
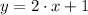 .
.