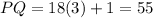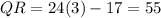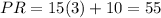Question

If PQR is an equilateral triangle, PQ=18x+1, QR=24x-17, and PR=15x+10, find x and the measure of each side.

Answer 1

The value of x is 3. The length of PQ, QR and PR are 55.

Explanation:

Given that the lengths in an equilateral triangle are all the same. We can assume that PQ = QR = PR. So we can choose any 2 lengths and compare it :

`PQ = QR`

`18x + 1 = 24x - 17`

`1 + 17 = 24x - 18x`

`6x = 18`

`x = 18 / 6`

`x = 3`

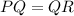
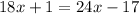
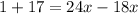
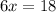
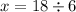
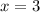
Next, we have to substitute x = 3 into the expressions :

`PQ = 18(3) + 1 = 55`

`QR = 24(3) - 17 = 55`

`PR = 15(3) + 10 = 55`

Answer 2

QR= PQ= PR

18x+1= 24x-17

18x-24x= -17-1

-6x= -18

x= 3

QR= 24(3)-17= 55

PQ= 18(3)+1= 55

PR= 15(3)+10=55