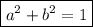Question

A sin^3theta+b cos^3theta=sintheta costheta and a sintheta-b costheta=0 then prove a^2+b^2=1​

Answer 1

Proof in explanation

Explanation:

Trigonometric Identities

The basic trigonometric identity is:

`\sin^2\theta+\cos^2\theta=1`

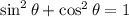
We'll use it and some basic algebra to prove that, given:

`a sin^3\theta+b cos^3\theta=sin\theta cos\theta`

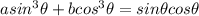
And

`a\sin\theta-b\cos\theta=0`

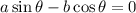
Then

`a^2+b^2=1`

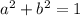
From the equation:

`a\sin\theta-b\cos\theta=0`

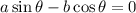
We have:

`a\sin\theta=b\cos\theta\qquad [1]`

The equation

`a sin^3\theta+b cos^3\theta=sin\theta cos\theta`

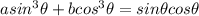
Can be rewritten as

`a\sin\theta \sin^2\theta+b \cos^3\theta=\sin\theta \cos\theta`

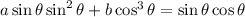
Replacing [1]:

`b\cos\theta \sin^2\theta+b \cos^3\theta=\sin\theta \cos\theta`

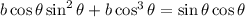
Taking the common factor:

`b\cos\theta (\sin^2\theta+ \cos^2\theta)=\sin\theta \cos\theta`

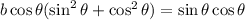
The expression in parentheses is 1, thus:

`b\cos\theta =\sin\theta \cos\theta`

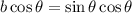
Dividing by
`\cos\theta`

`b=\sin\theta`

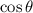
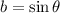
Replacing in

`a\sin\theta=b\cos\theta`

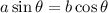
We have

`a\sin\theta=\sin\theta\cos\theta`

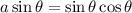
Dividing by
`\sin\theta`

`a=\cos\theta`

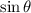
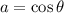
Now:

`a^2+b^2=(\cos\theta)^2+(\sin\theta)^2`

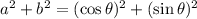
This expression is 1, thus it's proven:

`\boxed{a^2+b^2=1}`