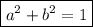Question

asked Jul 20, 2021 83.1k views

1 Answer

Roko Mijic · Answer 1 · 2021-07-27T17:41:07+0000

Answer:

Proof in explanation

Explanation:

Trigonometric Identities

The basic trigonometric identity is:

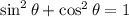
$\sin^2\theta+\cos^2\theta=1$

We'll use it and some basic algebra to prove that, given:

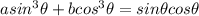
$a sin^3\theta+b cos^3\theta=sin\theta cos\theta$

And

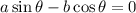
$a\sin\theta-b\cos\theta=0$

Then

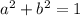
a^2+b^2=1

From the equation:

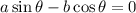
$a\sin\theta-b\cos\theta=0$

We have:

$a\sin\theta=b\cos\theta\qquad [1]$

The equation

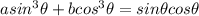
$a sin^3\theta+b cos^3\theta=sin\theta cos\theta$

Can be rewritten as

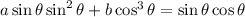
$a\sin\theta \sin^2\theta+b \cos^3\theta=\sin\theta \cos\theta$

Replacing [1]:

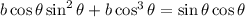
$b\cos\theta \sin^2\theta+b \cos^3\theta=\sin\theta \cos\theta$

Taking the common factor:

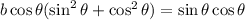
$b\cos\theta (\sin^2\theta+ \cos^2\theta)=\sin\theta \cos\theta$

The expression in parentheses is 1, thus:

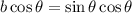
$b\cos\theta =\sin\theta \cos\theta$

Dividing by
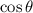
$\cos\theta$

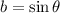
$b=\sin\theta$

Replacing in

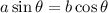
$a\sin\theta=b\cos\theta$

We have

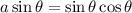
$a\sin\theta=\sin\theta\cos\theta$

Dividing by
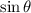
$\sin\theta$

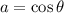
$a=\cos\theta$

Now:

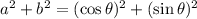
$a^2+b^2=(\cos\theta)^2+(\sin\theta)^2$

This expression is 1, thus it's proven:

$\boxed{a^2+b^2=1}$

Please log in or register to add a comment.