Answer:
B
Explanation:
We are given the two functions:
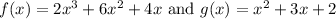
And we want to find which of the given polynomials are divisble by (2x + 3).
First, let's factor each of the functions:
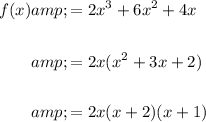
Likewise:
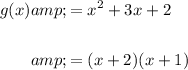
Let's see what happens if we add them together. This yields:
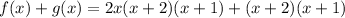
Rewriting:
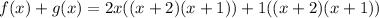
Factoring:
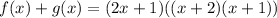
Therefore, we can see that since (2x + 1) is a factor, the expression is divisible by (2x + 1).
Then to make it divisible by (2x + 1), we can multiply g by three. This yields:
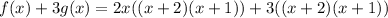
Rewriting:
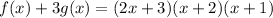
Since we now have a (2x + 3) term, the polynomial is now divisible by (2x + 3).
Therefore, our answer is B.