F(x)=2x^3+6x^2+4x g(x)=x^2+3x+2 The polynomials f(x) and g(x) are defined above. Which of the following polynomials is divisible by 2x+3? A) h(x) = f(x) + g(x) B) p(x) = f(x) + …

Question

asked Feb 6, 2021 139k views

2 Answers

Disbeliever · Answer 1 · 2021-02-10T04:45:27+0000

Answer:

B

Explanation:

We are given the two functions:

$f(x)=2x^3+6x^2+4x\text{ and } g(x)=x^2+3x+2$

And we want to find which of the given polynomials are divisble by (2x + 3).

First, let's factor each of the functions:

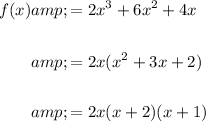
$\displaystyle \begin{aligned} f(x) &= 2x^3+6x^2+4x\\ \\ &= 2x(x^2+3x+2) \\ \\ &= 2x(x+2)(x+1)\end{aligned}$

Likewise:

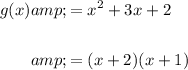
$\displaystyle \begin{aligned} g(x)&=x^2+3x+2\\ \\&= (x+2)(x+1)\end{aligned}$

Let's see what happens if we add them together. This yields:

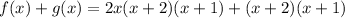
f(x)+g(x)=2x(x+2)(x+1)+(x+2)(x+1)

Rewriting:

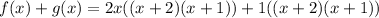
f(x)+g(x)=2x((x+2)(x+1))+1((x+2)(x+1))

Factoring:

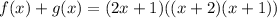
f(x)+g(x)=(2x+1)((x+2)(x+1))

Therefore, we can see that since (2x + 1) is a factor, the expression is divisible by (2x + 1).

Then to make it divisible by (2x + 1), we can multiply g by three. This yields:

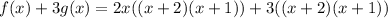
f(x)+3g(x)=2x((x+2)(x+1))+3((x+2)(x+1))

Rewriting:

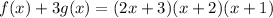
f(x)+3g(x)=(2x+3)(x+2)(x+1)

Since we now have a (2x + 3) term, the polynomial is now divisible by (2x + 3).

Therefore, our answer is B.