Question

AP CAL AB HELP!!!!!!!!!!!

Answer 1

Answer:With what does though

Explanation:

Answer 2

`(dx)/(dt)=0`

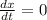
Explanation:

We have:

`y^2+xy-3x=8`

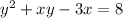
Where both x and y are functions of t.

To find our solution, let's first take the derivative of both sides with respect to t:

`(d)/(dt)[y^2+xy-3x]=(d)/(dt)[8]`

Expand:

`(d)/(dt)[y^2]+(d)/(dt)[xy]+(d)/(dt)[-3x]=(d)/(dt)[8]`

Differentiate. We must differentiate implicitly. Also, for the second term, we must use the product rule. So:

`(2y(dy)/(dt))+((dx)/(dt)y+x(dy)/(dt))-(3(dx)/(dt))=0`

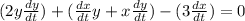
Simplify:

`2y(dy)/(dt)+(dx)/(dt)y+x(dy)/(dt)-3(dx)/(dt)=0`

We know that dy/dt is 3 when x is -4 and y is 2.

So, to find dx/dt, substitute 3 for dy/dt, -4 for x, and 2 for y. This yields:

`2(2)(3)+(dx)/(dt)(2)+(-4)(3)-3(dx)/(dt)=0`

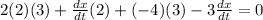
Simplify:

`12+2(dx)/(dt)-12-3(dx)/(dt)=0`

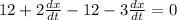
Simplify:

`-(dx)/(dt)=0`

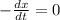
Divide both sides by -1:

`(dx)/(dt)=0`

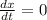
最终答案是零 :)