Answer:
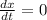
Explanation:
We have:
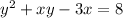
Where both x and y are functions of t.
To find our solution, let's first take the derivative of both sides with respect to t:
![(d)/(dt)[y^2+xy-3x]=(d)/(dt)[8]](https://img.qammunity.org/2021/formulas/mathematics/high-school/33celdvr0mya1dcgtn0iebut84tvjwi93z.png)
Expand:
![(d)/(dt)[y^2]+(d)/(dt)[xy]+(d)/(dt)[-3x]=(d)/(dt)[8]](https://img.qammunity.org/2021/formulas/mathematics/high-school/9ls0yg1jwpficns2lc768ip1234nyci39a.png)
Differentiate. We must differentiate implicitly. Also, for the second term, we must use the product rule. So:
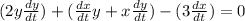
Simplify:
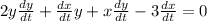
We know that dy/dt is 3 when x is -4 and y is 2.
So, to find dx/dt, substitute 3 for dy/dt, -4 for x, and 2 for y. This yields:
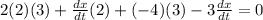
Simplify:
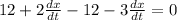
Simplify:
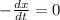
Divide both sides by -1:
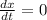
最终答案是零 :)