Question

The day Sunshine City was formed, it had a population of 100 people. However, the city grew exponentially over the following years. Its population could be modeled by this equation: , where p represents population, and t represents the time in years.

(1) What is the theoretical domain for Sunshine City’s population equation?

(2) What is the theoretical range for Sunshine City’s population equation?

(3) Assuming the model holds true, how many people will live in Sunshine City 20 years after it was founded? Round to the nearest tenth, and be sure to label your answer.

(4) Look at your answer to 2(c). Is it part of the practical range of the function? Why or why not? Explain the difference between the practical range and theoretical range of the function.

Answer 1

See below.

Explanation:

We know that Sunshine City was formed with a starting population of 100 people.

The city grew exponentially over the years, which can be modeled by the equation:

`P=100\cdot1.03^t`

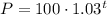
Where P represents the population and t represent the time in years.

Part 1)

The theoretical domain is simply the domain of our equation without any context.

In other words, we just need to find our domain like normally.

Our equation is:

`P=100\cdot1.03^t`

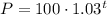
Since this is an exponential function, our domain will be all real numbers.

Therefore, our theoretical domain is all real numbers.

Part 2)

Similarly, our theoretical range is simply the range of our equation without any context.

We have the equation:

`P=100\cdot 1.03^t`

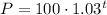
To find our range, we can graph our function. Refer to the graph below.

We can see that our range is all real numbers greater than 0.

However, note that we have a horizontal asymptote at y=0, so our y will never be exactly 0.

So, our theoretical range is all numbers greater than 0.

Part 3)

To find the amount of people living in Sunshine City after 20 years, we simply need to use our equation:

`P=100\cdot 1.03^t`

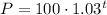
To find the population after 20 years, substitute 20 for t. So:

`P=100\cdot 1.03^(20)`

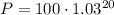
Use a calculator:

`P\approx180.6`

So, there will be about 180 people in Sunshine City after 20 years.

Part 4)

First, let's determine the practical range of our function.

Our theoretical range is all numbers greater than 0 because that's what the graph can output for any input.

However, our practical range will take into account the context.

Since our initial population was 100 and it grew each year, our range should never go below 100.

Therefore, our practical range is all values greater than or equal to 100.

We acquired approximately 180.6. Our answer is within our practical range, so we can indeed use our answer.

The main difference between theoretical range and practical range is that theoretical range doesn't take into account context while the practical range does. We know that we started with 100 people, so our range should be greater than that. This is our practical range. Our practical range will be based upon our practical domain, which in this case will be all numbers greater than 0 since we can't have negative years.