Answer:
see explanation
Explanation:
given a polynomial has roots x = a and x = b , then the corresponding factors are
(x - a) and (x - b)
the polynomial is then the product of the factors , that is
f(x) = (x - a)(x - b)
note that radical and complex roots occur in conjugate pairs.
(5)
given x = - 3i is a root then x = 3i is also a root
factors then are (x - 3i) , (x + 3i) , (x - 7) , then
f(x) = (x - 7)(x - 3i)(x + 3i) ← expand 2nd pair using foil
= (x - 7)(x² - 9i²) [ i² = - 1 ]
= (x - 7)(x² + 9) ← distribute factors
= x³ + 9x - 7x² - 63
f(x) = x³ - 7x² + 9x - 63
(6)
roots are x =
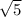 , x = -
, x = -
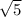 , x = i , x = - i , and factors are
, x = i , x = - i , and factors are
(x -
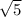 ) , (x +
) , (x +
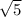 ) , (x - i) , (x + i) and
) , (x - i) , (x + i) and
f(x) = (x -
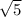 )(x +
)(x +
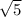 )(x - i)(x + i) ← expand pairs of factors using FOIL
)(x - i)(x + i) ← expand pairs of factors using FOIL
= (x² - 5)(x² + 1) ← distribute factors
=
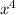 + x² - 5x² - 5
+ x² - 5x² - 5
then
f(x) =
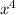 - 4x² - 5
- 4x² - 5