Question

A 134.0 g sample of an unknown metal is heated to 91.0⁰C and then placed in 125 g (125 mL) of water at 25.0⁰C. The final temperature of the water is measured at 31.0⁰C. Calculate the specific heat capacity of the unknown metal.

Answer 1

The specific heat capacity of the metal is approximately 0.3903 J/(g·°C)

Step-by-step explanation:

The mass of the sample of the unknown metal,
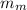`m_m` = 134.0 g

The temperature to which the metal is raised,
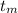`t_m` = 91.0°C

The mass of water into which the mass of metal is placed,
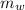`m_w` = 125 g

The temperature of the water into which the metal is placed,
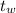`t_w`= 25.0°C

The final temperature of the water,
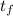`t_f` = 31.0°C

The specific heat capacity of water,
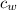`c_w` = 4.184 J/(g·°C)

The specific heat capacity of the metal =
`c_m`

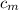
Therefore, by the first laws of thermodynamics we have;

The heat transferred = Heat supplied by the metal = Heat gained by the water

The heat transferred, ΔQ, is given as follows;

ΔQ =
`m_w`×
`c_w`×(
`t_f` -
`t_w`) =
`m_m`×
`c_m`×(
`t_m` -
`t_f`)

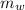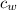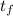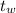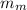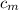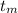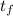125 × 4.184 × (31 - 25) = 134 ×
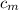`c_m` × (91 - 31)

∴
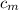`c_m` = (125 × 4.184 × (31 - 25))/(134 × (91 - 31)) ≈ 0.3903 J/(g·°C)

The specific heat capacity of the metal =
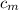`c_m` ≈ 0.3903 J/(g·°C)