Question

Determine whether a triangle can be formed with the given side lengths. If so, use Heron's formula to find the area of the triangle. a = 240 b = 132 c = 330

Answer 1

a, b, and c can be formed a triangle

The area of the triangle is 13385.87 square units.

Explanation:

Let us revise an important fact in any triangle

• The sum of the lengths of the two shortest side must be greater than the length of the longest side

The length of the sides are a = 240, b = 132, and c = 330

∵ The two shortest sides are a = 240 and b = 132

∵ a + b = 240 + 132 = 372

∵ The longest side is c = 330

∵ 372 > 330

∴ a + b > c

∴ a, b, and c can be formed a triangle

Let us revise the Heron's formula of the area of the triangle

• Area =
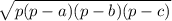  `√(p(p-a)(p-b)(p-c))`, where a, b,c are the lengths of the sides of the triangle, and
  `p=(a+b+c)/(2)`

∵
`p=(240+132+330)/(2)=351`

∴
`Area = √(351(351-240)(351-132)(351-330))`

∴
`Area = √(351(111)(219)(21))`

∴
`Area=13385.87`

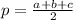
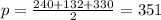
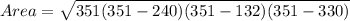
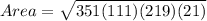
The area of the triangle is 13385.87 square units.