Answer:
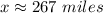
Explanation:
Linear Modeling
Some events can be modeled as linear functions. If we are in a situation where a linear model is suitable, then we need two sample points to make the model and predict unknown behaviors.
The linear function can be expressed in the slope-intercept format:
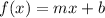
For the problem at hand, we must pick the adequate variables according to the data provided.
The question states the charge for renting a car is a function of the mileage. It also provides two points from which we can build our model. Let's set the following variables:
c = the charge for renting a car in dollars
x = the distance driven by the businessman in miles
Representing the ordered pair as (x,c), we have the points: (150,79) and (65,63.70). Our model will be expressed as:
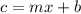
We must find the values of m and b with the data provided. Substituting the first point:
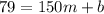
Substituting the second point:
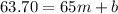
Both equations form the following system:
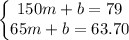
Subtracting both equations:
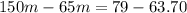
Note the variable b was canceled out in the operation, leaving only the variable m to solve. Joining like terms:
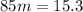
Solving:
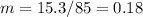
From the first equation
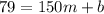
Solving for b:
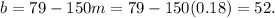
The model for the problem is:

Now we need to calculate how many miles (x) could be driven for c=$100. From the equation above, substitute c=100
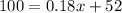
Solve for x:

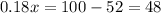
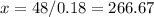
Rounding to the closest integer:
