Question

Which table describes a linear function that has a slope of 2?​

Answer 1

Table (4)

Explanation:

Slope of a line passing through two points
`(x_1,y_1)` and
`(x_2,y_2)` is,

m =
`(y_2-y_1)/(x_2-x_1)`

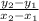
From the table (1),

Two points lying on the graph are (2, 1) and (6, -1).

Slope of the line =
`(1+1)/(2-6)` =
`-(1)/(2)`

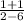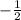
From the table (2),

Two points lying on the linear function are (0, 8) and (2, 4).

Slope of the line =
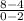`(8-4)/(0-2)` = -2

From the table (3),

Two points are (-4, 4) and (-2, 5).

Slope of the line =
`(5-4)/(-2+4)` =
`(1)/(2)`

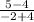From table (4),

Two points lying on the function are (-2, 0) and (0, 4).

Slope of the line =
`(4-0)/(0+2)=2`

Therefore, Table (4) represents a linear function with slope 2.