Answer:
Geometric series are seen in practical situations, most notably in those involving geometric growth or decay. If a series of numbers are formed by percentages, then it can result in a geometric sequence. Ex. compound interest (see below).
Explanation:
A geometric series is the result of adding the terms of a geometric sequence. These sequences have a common ratio, r, which is used to find missing terms. The common ratio is found with
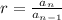 . For example,
. For example,
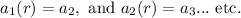
Geometric sequences can be used to model practical situations, and such situation could involve geometric growth or decay.
A geometric sequence can be used to model compound interest. An example of this is
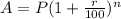 where the common ratio, r, of the series is equal to 1 + r/100 in the compound interest formula above.
where the common ratio, r, of the series is equal to 1 + r/100 in the compound interest formula above.