Question

What are practical situations of geometric series.

Answer 1

Geometric series are seen in practical situations, most notably in those involving geometric growth or decay. If a series of numbers are formed by percentages, then it can result in a geometric sequence. Ex. compound interest (see below).

Explanation:

A geometric series is the result of adding the terms of a geometric sequence. These sequences have a common ratio, r, which is used to find missing terms. The common ratio is found with
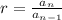`r=(a_n)/(a_(n-1))`. For example,
`a_1(r)=a_2, \mbox{ and } a_2(r)=a_3... \mbox{ etc.}`

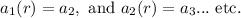
Geometric sequences can be used to model practical situations, and such situation could involve geometric growth or decay.

A geometric sequence can be used to model compound interest. An example of this is
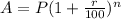`A = P (1 + (r)/(100))^n` where the common ratio, r, of the series is equal to 1 + r/100 in the compound interest formula above.

Answer 2

One of the practical situation of geometric series is : A ball bouncing is an example of a finite geometric sequence. Each time the ball bounces it’s height gets cut down by half. If the ball’s first height is 4 feet, the next time it bounces it’s highest bounce will be at 2 feet, then 1, then 6 inches and so on, until the ball stops bouncing