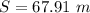Answer:
a
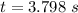
b
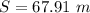
Step-by-step explanation:
From the question we are told that
The height of the helicopter is
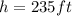
The height of the bed of the truck is
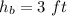
The speed of the truck is
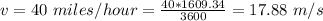
Generally the distance between the truck bed and the helicopter is mathematically represented as
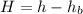
=>
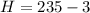
=>

Converting to meters
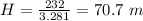
Generally the time at which the helicopter should drop the package is mathematically represented as
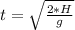
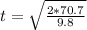
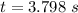
Generally distance of the helicopter from the drop site at time t = 0 s is
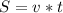
=>
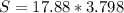
=>