Question

You have landed a summer job as the technical assistant to the director of an adventure movie shot here in Arizona. The script calls for a large package to be dropped onto the bed of a fast moving pick-up truck from a helicopter that is hovering above the road, out of view of the camera. The helicopter is 235 feet above the road, and the bed of the truck is 3 feet above the road. The truck is traveling down the road at 40 miles/hour. You must determine when to cue the assistant in the helicopter to drop the package so it lands in the truck. The director is paying $20,000 per hour for the chopper, so he wants you to do this successfully in one take. If t = 0 is the time that filming starts at and you can assume that the truck is already at speed, at what time should the helicopter release the package and how far back from the drop site should it be at t = 0?

Answer 1

a

`t = 3.798 \  s`

b

`S = 67.91 \ m`

Step-by-step explanation:

From the question we are told that

The height of the helicopter is
`h= 235 ft`

The height of the bed of the truck is
`h_b = 3 \ ft`

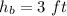
The speed of the truck is
`v = 40 \ miles / hour = (40 * 1609.34)/(3600) = 17.88 \ m/s`

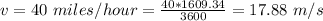
Generally the distance between the truck bed and the helicopter is mathematically represented as

`H = h - h_b`

=>
`H = 235 -3`

=>
`H = 232 \ ft`

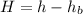
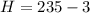
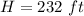
Converting to meters

`H = ( 232)/(3.281) = 70.7 \ m`

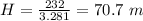
Generally the time at which the helicopter should drop the package is mathematically represented as

`t = \sqrt{(2 * H)/(g) }`

`t = \sqrt{(2 * 70.7)/(9.8) }`

`t = 3.798 \ s`

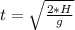
Generally distance of the helicopter from the drop site at time t = 0 s is

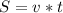
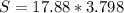
`S = v * t`

=>
`S =  17.88   *  3.798`

=>
`S = 67.91 \ m`