Answer:
From the question we are told that
The equation is
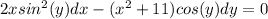
Generally the goal of this solution is to prove that the implicit solution of the differential equation above is

First Step
Differentiate the solution with respect to x
/(dx)](https://img.qammunity.org/2021/formulas/mathematics/college/23ys79bvsnf0l39o90a7lrvki4ygcxvk5s.png)
=>
/(dx)](https://img.qammunity.org/2021/formulas/mathematics/college/r5vgtj19venejxqy3d80we41d71zlj4fg1.png)
=>
/(dx)](https://img.qammunity.org/2021/formulas/mathematics/college/xkqx1cw8uy8u1k7ibux01qg07ssyq2fpv1.png)
=>
multiply through by
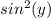 ,
,
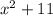 ,
,
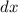
So
=>
![2 x (sin^2(y) dx + [-cos(y) (x^2 + 11)]dy = 0](https://img.qammunity.org/2021/formulas/mathematics/college/wb5ouoe44p0f5u0o6x3xk5yxeghxmmyszd.png)
Looking at the equation obtained we see that it is equivalent to the differential equation hence the implicit solution of
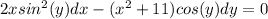 is
is

Explanation: