Question

Imagine there are two series of science-fictions: The Three-Body Problem (T) and Galactic Empires (G). Your utility function is U = TG, where T is the number of books you consume for The Three-Body Problem, and G is the number of books you consume for Galactic Empires. If your budget is $200, the price of each book of The Three-Body Problem (T) is $50, and the price of each book of Galactic Empires (G) is $100, how many books of The Three-Body Problem (T) will you consume?

Answer 1

With a $200 budget, $50 per book for The Three-Body Problem and $100 per book for Galactic Empires, the optimal allocation for maximum utility (U = TG) is to buy 2 books of The Three-Body Problem and 1 book of Galactic Empires.

To maximize your utility function U = TG with a budget constraint, you want to allocate your budget in a way that maximizes the product of T and G.

Let's denote:

- x as the number of books of The Three-Body Problem (T)

- y as the number of books of Galactic Empires (G)

The total cost of books is given by the budget constraint:

`\[50x + 100y \leq 200\]`

To maximize U = TG, you want to maximize the product xy.

Now, let's set up the problem:

Objective function: U = xy

Subject to the constraint:
`\( 50x + 100y \leq 200 \)`

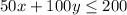
To simplify, you can rewrite the constraint as:

`\[ x + 2y \leq 4 \]`

Now, you need to find the values of x and y that satisfy this constraint and maximize U.

Since your utility function is U = TG, you want to allocate your budget in a way that maximizes the product of the number of books from each series.

Given the constraint
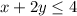`\( x + 2y \leq 4 \)`, let's consider some possible solutions:

1. If you buy 2 books of The Three-Body Problem (x = 2), then
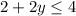`\( 2 + 2y \leq 4 \)`, and you can buy one book of Galactic Empires (y = 1).

2. If you buy 4 books of The Three-Body Problem (x = 4), then
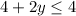`\( 4 + 2y \leq 4 \)`, and you cannot buy any books of Galactic Empires.

So, it seems that the maximum utility is achieved when you buy 2 books of The Three-Body Problem and 1 book of Galactic Empires.

Therefore, you would consume 2 books of The Three-Body Problem.

Answer 2

2 books

Step-by-step explanation:

your utility function is:

F(U) = TG

In order to maximize your utility you must at least buy 1 book of the Three-Body Problem (T) and 1 book of the Galactic Empires (G). The constraint here is that both T and G must be ≥ 1. Since your budget is only $200, the maximum number of G books that you can buy is 1, or you wouldn't have any money left to buy T books.

So you purchase 1 G book and you have $100 left which you can use to purchase 2 T books.