Answer:
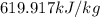
Step-by-step explanation:
As the tank is closed and rigid, so, the mass inside the tank is fixed and the volume,
 , remains constant which is
, remains constant which is

For the pressure, P=2 bar, the thermodynamic state of ammonia on the boiling curve are
The specific volume of the liquid ammonia,

The specific volume of the vapor ammonia,
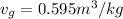
The specific enthalpy of the liquid ammonia,
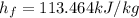
The specific enthalpy of the vapor ammonia,
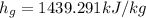
At pressure, P=4 bar
The given specific volume,
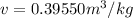 .
.
Let
 and
and
 be the specific volumes of Ammonia in the tank. As the tank is closed, so there is no flow of Ammonia to or from the tank. Hence the mass remains constant. Also, the volume of the tank is constant, so the specific volume of Ammonia in the tank remains constant.
be the specific volumes of Ammonia in the tank. As the tank is closed, so there is no flow of Ammonia to or from the tank. Hence the mass remains constant. Also, the volume of the tank is constant, so the specific volume of Ammonia in the tank remains constant.
Hence,
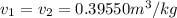
Let
 be the vapor quality for initial condition, so
be the vapor quality for initial condition, so
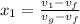
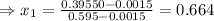
So, the initial specific energy, the liquid-vapor mixture of Ammonia have, is
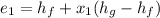
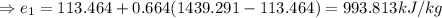
Now, at pressure, P=4 bar and
 , total amount exist in the vapor phase having the specific enthalpy
, total amount exist in the vapor phase having the specific enthalpy
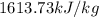
So, the final energy, Ammonia have, is
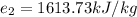
So, change in energy per kilogram of Ammonia is
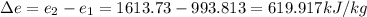 .
.
As the change of kinetic and potential energy are negligible and work done by the system (Ammonia in the tank) is zero due to the rigid tank, so the energy added to the tank can cause only change in energy of the system (Ammonia in the tank).
Hence, the amount of energy transfer by heat
 .
.