Question

A. One week, Park Street's revenues were $7500, which was the 15th highest revenue recorded for that restaurant. In the same wook, Bridge Road's

revenue was $7100, the 12th highest for that restaurant Use percentiles and 7-scores to compare how successful each restaurant was that wook,
relative to their typical weekly revenue

Answer 1

The percentile rank for Park Street's revenues this week is 60th.

The percentile rank for Bridge Road's revenues this week is 73rd.

Explanation:

The missing information are as follows:

Variable N Mean SD

Park 36 6611 3580

Bridge 40 5989 1794

A z-score (aka, a standard score) specifies the number of standard deviations an observation is from the mean.

The formula to compute the z-score is,
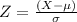`Z = ((X - \mu))/(\sigma)`, where X = observation, µ = mean, σ = standard deviation.

Compute the z-score for Park Street's revenues, $7500 as follows:

`Z_(p) = ((X - \mu))/(\sigma)=(7500-6611)/(3580)=0.25`

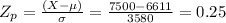
The z-score for Park Street's revenues this week is 0.25.

Compute the percentile rank for Park Street's revenues this week as follows:

`P(Z<Z_(p))=P(Z<0.25)=0.5987\approx 0.60\ \text{or}\ 60\%`

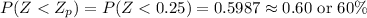
The percentile rank for Park Street's revenues this week is 60th.

This implies that the Park Street's performed better than 60% of the revenue recorded for the restaurant.

Compute the z-score for Bridge Road's revenues, $7100 as follows:

`Z_(p) = ((X - \mu))/(\sigma)=(7100-5989)/(1794)=0.62`

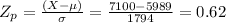
The z-score for Bridge Road's revenues this week is 0.62.

Compute the percentile rank for Bridge Road's revenues this week as follows:

`P(Z<Z_(b))=P(Z<0.62)=0.7324\approx 0.73\ \text{or}\ 73\%`

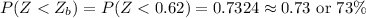
The percentile rank for Bridge Road's revenues this week is 73rd.

This implies that the Bridge Road's performed better than 73% of the revenue recorded for the restaurant.