Answer:
Part A)
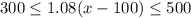
Part B)

Nate wants the original price of the laptop to be between approximately $378 or $563.
Explanation:
Part A)
Let's let x be the price of the new laptop.
Since the store is offering a $100 rebate (discount), this means that the total cost of the laptop before tax is:
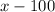
So, the total price of the laptop after the 8% tax is:
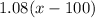
Since Nate is planning to spend between $300 and $500, this means that we can write the following compound inequality:
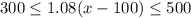
Part B)
To find the range of the price of laptops, let's find the solution to our inequality.
To do so, let's solve them individually. So, let's first find our minimum price:
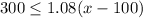
Divide both sides by 1.08:

Add 100 to both sides:
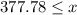
So, Nate wants the laptop to be at least approximately $378.00.
Now, let's find our maximum price:
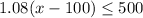
Divide both sides by 1.08:

Add 100 to both sides:

So, Nate wants the maximum price of the laptop to be about $563.00.
So, our compound inequality is:

This means that Nate wants the original price of the laptop to be between approximately $378 or $563.
And we're done!