Question

(2x2 + 4x - 3)(x2 - 2x + 5)

2x4 + 7x2 - 15
2x4 - 8x2 - 15
2x4 - x2 + 26x - 15

2x4 + 8x3 - x2 + 26x - 15

Answer 1

This is the answer 2x4 - x2 + 26x - 15

Explanation:

Answer 2

The answer is (C)

Explanation:

Let us multiply the two trinomials and simplify the product to find the correct choice.

`(2x^(2)+4x-3)(x^(2)-2x+5)`

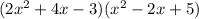
To find the product multiply each term in the first bracket by the second bracket, then add the like terms

`2x^(2) (x^(2)-2x+5)=2x^(2)(x^(2))+2x^(2)(-2x)+2x^(2)(5)=2x^(4)-4x^(3)+10x^(2)`

`4x(x^(2)-2x+5)=4x(x^(2))+4x(-2x)+4x(5)=4x^(3)-8x^(2)+20x`

`(-3)(x^(2)-2x+5)=(-3)(x^(2))+(-3)(-2x)+(-3)(5)=-3x^(2)+6x-15`

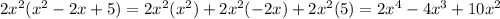
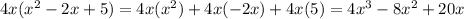
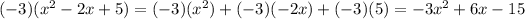
Now let us add the like terms.

`2x^(4)-4x^(3)+10x^(2)+4x^(3)-8x^(2)+20x-3x^(2)+6x-15=`

`2x^(4)+(-4x^(3)+4x^(3))+(10x^(2)-8x^(2)-3x^(2))+(6x+20x)-15=`

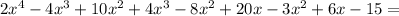
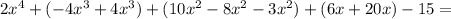
Simplify each term

`2x^(4)+(0)x^(3)-x^(2)+26x-15=`

`2x^(4)-x^(2)+26x-15`

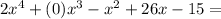
By comparing it with the choices

The answer is (C)