Determine which ordered pair(s) lie on the function f(x)=(1/4)^x. (1,4) (-1,4), (3, 1/64), (0, 1/4)

Question

asked May 17, 2021 229k views

1 Answer

Donaldo · Answer 1 · 2021-05-21T19:06:35+0000

Given:

The function is

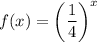
$f(x)=\left((1)/(4)\right)^x$

To find:

The ordered pair(s) from the options lie on the function.

Solution:

We have,

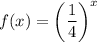
$f(x)=\left((1)/(4)\right)^x$

For x=1,

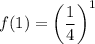
$f(1)=\left((1)/(4)\right)^1$

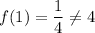
$f(1)=(1)/(4)\\eq 4$

So, the point (1,4) does not lies on the function f(x).

For x=-1,

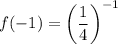
$f(-1)=\left((1)/(4)\right)^(-1)$

f(-1)=4

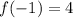
So, the point (-1,4) lies on the function f(x).

For x=3,

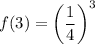
$f(3)=\left((1)/(4)\right)^(3)$

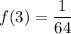
f(3)=(1)/(64)

So, the point
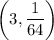$\left(3,(1)/(64)\right)$ lies on the function f(x).

For x=0,

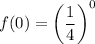
$f(0)=\left((1)/(4)\right)^0$

f(0)=1

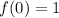
So, the point
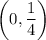$\left(0,(1)/(4)\right)$ does not lies on the function f(x).

Therefore, the correct options are B and C.