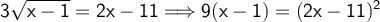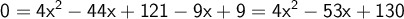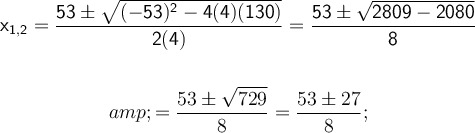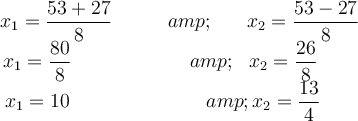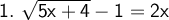
The root of the equation is solved first. Afterwards, both members of the equality are squared, the powers are developed and it is solved.

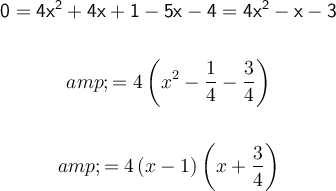
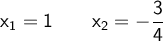
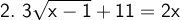
The root of the equation is cleared. Then, both sides of the equality are squared, the powers are developed and it is solved by the general formula.