Question

Problem: Report Error We have $64^{-1} = \frac{1}{64}.$ But $\frac{1}{64}$ can be written as an integer raised to an integer power in other ways, too! How many different ways in total can $\frac{1}{64}$ be written as an integer raised to an integer power, including $64^{-1}$?

Answer 1

4 different ways

Explanation:

Given
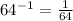`64^(-1) = (1)/(64)`, we are told that the expression cam also be written as an integer raised to an integer power in other ways, the other ways are as shown below;

First way:

`(2^6)^(-1) = 2^(-6)\\2^(-6) = (1)/(2^6) \\Hence \ 64^(-1) = 2^(-6)`

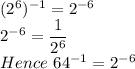
Second way:

`(64)^(-1) = (4^3)^(-1)\\4^(-3) = (1)/(4^3) \\Hence \ 64^(-1) = 4^(-3)`

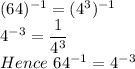
third way:

`(64)^(-1) = (8^2)^(-1)\\8^(-2) = (1)/(8^2) \\Hence \ 64^(-1) = 8^(-2)`

Therefore the expression
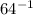`64^(-1)` can also be written as
`2^(-6), 4^(-3) \ and \ 8^(-2)`.

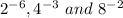The total number of different ways
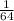`(1)/(64)` can be written including
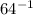`64^(-1)` is 4