Question

A dialysis unit is being designed. It will consist of a large number of small hollow fibers arranged in parallel. Blood will flow inside the fibers, each of which is 30 cm long. It is desired that the hold-up volume (the volume of blood needed to fill all the fibers) should be no more than 80 ml, and that the total pressure drop across the fibers should be no more than 105 dyne/cm2 at a total flow rate of 50 ml/s. If the blood viscosity is 3.5 cP and the density of the blood is 1.05 g/cm3, how many fibers should be used, and of what diameter should they be, so as to meet the design conditions

Answer 1

Step-by-step explanation:

Given information:

A designed dialysis unit consists of a large no of small hollow fibers,

Considering the one fiber,

By using the volume of blood, we have :

`V =(\pi)/(4)* D^2 * L`

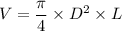
where:

L = 30cm = (30× 10) mm = 300 mm

Volume = 80 ml = 80 × 10³ mm

From the above equation, making D the subject, we have:

`4 V ={\pi}* D^2 * L`

`D^2 =\frac{4 V }{{\pi}* L}`

`D^2 =(4 * 80 * 10^3 )/( \pi * 300)`

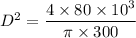
D² = 339.53

`D = √(339.53)`

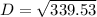
D = 18.43 mm

D = 1.843 cm

However, suppose we consider the laminar flow, the pressure loss in a single fiber can be determined as follows:

`\Delta p = \rho g h_f= (32* \mu *\overline u*l )/(D^2)`

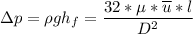
where;

`\overline u = (4 * 50 * 10^3)/(\pi * (18.43)^2)`

`\overline u = (200000)/(1067.088755)`

`\overline u =187.43 \ mm/sec`

`\overline u =18.743 \ cm/sec`

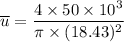
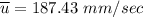
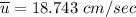
Recall:

`\Delta p = (32* \mu *\overline u*l )/(D^2)`

`\Delta p = (32* 3.5 * 10^(-2) *18.743*30 )/(1.843^2)`

`\Delta p = (629.7648 )/(3.396649)`

`\Delta p =185.41 \ dyne/cm^2`

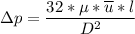
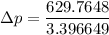
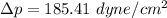
Finally, the number of needed to be used =
`(p)/(\Delta p)`

=
`(10^5 \ dyne /cm^2)/(185.41\ dyne /cm^2)`

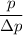
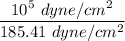
= 539.35