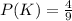Question

Consider the following 9 door version of the Monty Hall problem. There are 9 doors, behind one of which there is a car (which you want), and behind the rest of which there are goats (which you don’t want). 1 2 Initially, all possibilities are equally likely for where the car is. You choose a door. Monty Hall then opens 4 goat doors, and offers you the option of switching to any of the remaining 4 doors. Assume that Monty Hall knows which door has the car, will always open 4 goat doors and offer the option of switching, and that Monty chooses with equal probabilities from all his choices of which goat doors to open. Should you switch? What is your probability of success if you switch to one of the remaining 4 doors?

Answer 1

In the 9 door version of the Monty Hall problem, it is advantageous to switch doors. The probability of success if you switch to one of the remaining 4 doors is 4/9 or approximately 0.4444.

Step-by-step explanation:

In the 9 door version of the Monty Hall problem, it is advantageous to switch doors. Initially, the car has an equal probability of being behind any of the 9 doors. After Monty Hall opens 4 goat doors, you should switch because the probability of the car being behind one of the remaining 4 doors is higher than the door you initially chose.

If you switch to one of the remaining 4 doors, your probability of success is 4/9 or approximately 0.4444.

Answer 2

The probability of success if you switch to one of the remaining 4 doors is

`P(K) =(4)/(9)`

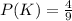
Step-by-step explanation:

From the question we are told that

The number of doors is n = 9

Generally the probability that the car is in the door you choose is

`P(C) = (1)/(9)`

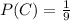
Generally the probability that the car is in the rest of the doors is

`P(C)' = (8)/(9)`

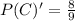
Given that Monty Hall opened the 4 goat doors then the probability that the car will be in the remaining 4 doors is mathematically evaluated as

`P(K) = (P(C)')/(2)`

=>
`P(K) =  ((8)/(9))/(2)`

=>
`P(K) =(4)/(9)`

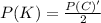
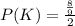
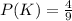
Thus the probability of success if you switch to one of the remaining 4 doors is

`P(K) =(4)/(9)`