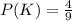Answer:
The probability of success if you switch to one of the remaining 4 doors is
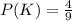
Step-by-step explanation:
From the question we are told that
The number of doors is n = 9
Generally the probability that the car is in the door you choose is
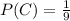
Generally the probability that the car is in the rest of the doors is

Given that Monty Hall opened the 4 goat doors then the probability that the car will be in the remaining 4 doors is mathematically evaluated as
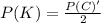
=>
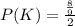
=>
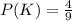
Thus the probability of success if you switch to one of the remaining 4 doors is