Question

Rationalize the denominator:

`(1)/( √(3) - √( 2) )`
​

Answer 1

√3 + √2

Explanation:

The best approach to this problem would be by multiplying the denominator ad numerator by the denominator's conjugate;

1(√3 + √2) / (√3 - √2)(√3 + √2)

= (√3 + √2) / (√3)^2 - (√2)^2

= √3 + √2 / 3 - 2

= √3 + √2 / 1 = √3 + √2

We now have a denominator of 1, which is rationalized. The solution would be √3 + √2.

Answer 2

________________________________

`step\:1`

`(1)/( √(3) - √(2) )`

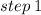
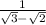
write the equation

________________________________

`step\:2`

`(1 * ( √(3) + √(2)) )/( (√(3) - √(2) ) * (√(3) + √(2)) )`

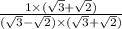
multiply both numerator and denominator by √3+√2

________________________________

`step\:3`

`( √(3) + √(2) )/( ( 3 ) - ( 2 ) )`

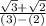
after multiplying numerator with √3+√2 we get→√3+√2

after multiplying denominator we get 3-2

________________________________

`step\:4`

`( √(3) + √(2) )/(1)`

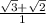
after subtracting 3 with 2 we get →1

________________________________

hence denominater is rationalized✓

hope it helped you:)