Answer:
________________________________
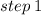
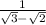
write the equation
________________________________
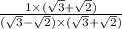
multiply both numerator and denominator by √3+√2
________________________________
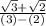
after multiplying numerator with √3+√2 we get→√3+√2
after multiplying denominator we get 3-2
________________________________
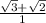
after subtracting 3 with 2 we get →1
________________________________
hence denominater is rationalized✓
hope it helped you:)