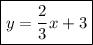Answer:
Explanation:
Perpendicular Bisector
It's defined as a line that divides another line into two equal parts. The bisector passes through the midpoint of the line forming any angle, but if that angle is exactly 90°, then the bisector is also perpendicular.
We need to find the equation of the line that divides into equal parts the line with endpoints (-1, -2) and (-5,4) and is perpendicular to it.
First, let's find the slope of the line segment. The slope can be calculated with the formula:
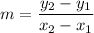

The line for the perpendicular bisector has a slope m2. Two perpendicular lines with slopes m1 and m2 must comply:
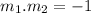
Solving for m2:
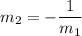
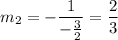
The equation of the perpendicular bisector has the form:

Now we find the coordinates of the midpoint of the segment:
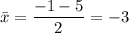

The midpoint is (-3,1). Using this point will allow us to find the value of b:

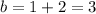
Thus, the equation for the perpendicular bisector is