Question

Solve the problem. If s is a distance given by s(t) = + + 40 + 10. find the acceleration, alt). Q ald) = 10 ald) = 2t + 4 O alt) = 2 O ald) = 2t​

Answer 1

C

Explanation:

Remember that if s(t) is a position function then:

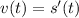`v(t)=s'(t)` is the velocity function and

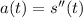`a(t)=s''(t)` is the acceleration function.

So, to find the acceleration, we need to solve for the second derivative of our original function. Our original function is:

`s(t)=t^2+4t+10`

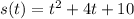
So, let's take the first derivative first with respect to t:

`(d)/(dt)[s(t)]=(d)/(dt)[t^2+4t+10]`

Expand on the right:

`s'(t)=(d)/(dt)[t^2]+(d)/(dt)[4t]+(d)/(dt)[10]`

Use the power rule. Remember that the derivative of a constant is 0. So, our derivative is:

`v(t)=s'(t)=2t+4`

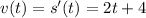
This is also our velocity function.

To find acceleration, we want to second derivative. So, let's take the derivative of both sides again:

`(d)/(dt)[s'(t)]=(d)/(dt)[2t+4]`

Again, expand the right:

`s''(t)=(d)/(dt)[2t]+(d)/(dt)[4]`

Power rule. This yields:

`a(t)=s''(t)=2`

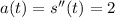
So, our answer is C.

And we're done!