Question

Evaluate the expression. 50 points!!

Answer 1

c

Explanation:

Answer 2

C

Explanation:

If you notice, this is what the tangent-difference identity resembles. The tangent-difference identity is:

`\tan(\alpha-\beta)=(\tan(\alpha)-\tan(\beta))/(1-\tan(\alpha)\tan(\beta))`

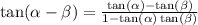
We have the expression:

`(\tan((\pi)/(7))-\tan((\pi)/(8)))/(1-\tan((\pi)/(7))\tan((\pi)/(8)))`

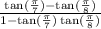
So, our α is π/7 and our β is π/8. Therefore:

`(\tan((\pi)/(7))-\tan((\pi)/(8)))/(1-\tan((\pi)/(7))\tan((\pi)/(8)))=\tan((\pi)/(7)-(\pi)/(8)})`

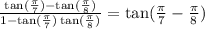
Simplify:

`(\tan((\pi)/(7))-\tan((\pi)/(8)))/(1-\tan((\pi)/(7))\tan((\pi)/(8)))=\tan((8\pi)/(56)-(7\pi)/(56)})`

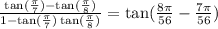
Subtract:

`(\tan((\pi)/(7))-\tan((\pi)/(8)))/(1-\tan((\pi)/(7))\tan((\pi)/(8)))=\tan((\pi)/(56))`

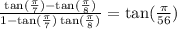
So, our answer is C.

And we're done!