Question

Continues (- infinity , infinity) find c

[ cx^2 + 8x
if x < 5
X^3 - cx if x> 5

Answer 1

It sounds like you're asked to find c such that f(x), defined by

`f(x)=\begin{cases}cx^2+8x&\text{for }x<5\\x^3-cx&\text{for }x>5\end{cases}`

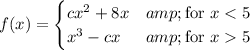
is continuous at x = 5.

With the strict inequalities given in the definition, this is not possible. So you probably meant to use ≤ or ≥ in one of the pieces of the definition.

In order for f(x) to be continuous at x = 5, the limit from either side as x approaches 5 must be the same.

We have

`\displaystyle\lim_(x\to5^-)f(x)=\lim_(x\to5)(cx^2+8x)=25c+40`

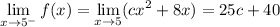
and

`\displaystyle\lim_(x\to5^+)f(x)=\lim_(x\to5)(x^3-cx)=125-5c`

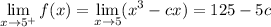
Then

`25c+40=125-5c\implies30c=85\implies c=(85)/(30)=\boxed{\frac{17}6}`