Answer:
19)
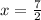
20)

Explanation:
19)
We have the function:

And we want to find x such that t(x)=0.
So, substitute 0 for t(x):
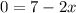
Solve for x. Subtract 7 from both sides:

Divide both sides by -2:
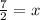
Flip:
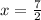
20)
We have:
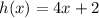
To find h(x+3), substitute (x+3) for x. This yields:
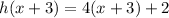
Multiply:

Add:

And we're done!