Answer:
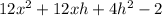
==================================================
Step-by-step explanation:
First let's find the expression f(x+h). We replace every copy of x with x+h, expand, and simplify like so.

This may look ugly, but things will simplify a bit when we subtract off f(x)
Note how in f(x+h) we have the following terms
Which are the exact terms found in f(x) as well.
Why is this important? It helps us subtract and cancel. When we subtract off f(x), we cross off the 4x^3 and -2x terms in that f(x+h) equation above.
We'll be left with this
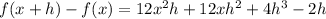
At this point, every term shown has at least one copy of 'h' as a factor.
This allows us to factor out h
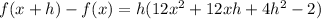
Then we can divide both sides by h to get our final answer
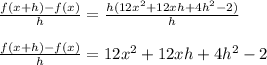
----------------------------------------------------
Extra info:
h is nonzero to avoid dividing by zero. Though as h gets closer and closer to zero, terms with h in them will drop out since those terms will be very small. We'll be left with 12x^2-2. This is the derivative of f(x).