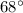Answer:
15.
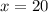
16.
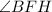 =
=
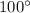
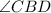 =
=
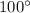 (if needed)
(if needed)
-------------------------------------------------------------------
17.
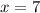
18.
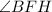 =
=
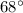
Explanation:
15. The two following angles, which is
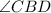 and
and
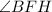 , are Corresponding Angles. Write an expression by using the following measurements from
, are Corresponding Angles. Write an expression by using the following measurements from
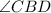 and
and
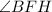 . Then, solve the expression for the value of
. Then, solve the expression for the value of
 :
:
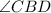 =
=
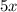
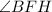 =
=
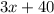
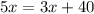
Solve for
 :
:
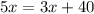
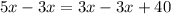
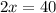
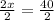
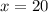
16. After you have the value
 use it to find the actual measurements of both
use it to find the actual measurements of both
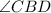 and
and
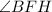 , by applying
, by applying
 to the following expressions from both
to the following expressions from both
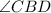 and
and
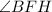 and solve them:
and solve them:
-The value of
 :
:
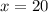
-Solve for
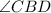 :
:
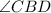 =
=
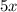
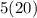
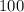
-The actual measurement of
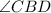 :
:
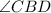 =
=
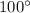
-Solve for
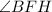 :
:
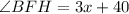
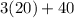
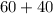
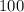
-The actual measurement of
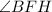 : (if needed)
: (if needed)
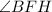 =
=
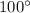
----------------------------------------------------------------------------
17. The two following angles, which is
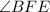 and
and
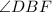 are Alternate Interior Angles .Write an expression by using the following measurements from
are Alternate Interior Angles .Write an expression by using the following measurements from
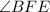 and
and
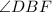 . Then, solve the expression for the value of
. Then, solve the expression for the value of
 :
:
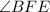 =
=
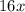
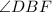 =
=
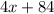
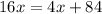
-Solve for
 :
:
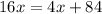
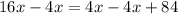
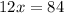

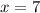
18. After you have the value
 use it to find the actual measurement of
use it to find the actual measurement of
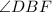 , by applying
, by applying
 to the expression from
to the expression from
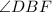 and solve it and find the actual measurement of an angle that is not labeled, which is
and solve it and find the actual measurement of an angle that is not labeled, which is
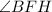 :
:
-The value of
 :
:
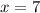
Solve for
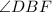 :
:
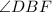 =
=
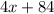
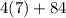
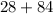
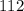
-The actual measurement of
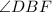 :
:
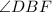 =
=
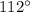
-Since both
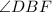 and
and
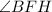 are supplementary (two angles that equals to
are supplementary (two angles that equals to
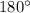 ), and you want to find the actual measurement of
), and you want to find the actual measurement of
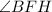 , Use the measurement of
, Use the measurement of
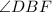 and subtract it from
and subtract it from
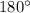 :
:
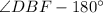
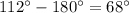
-The actual measurement of
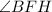 :
:
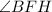 =
=