Question

One strategy in a snowball fight is to throw a snowball at a high angle over level ground. While your opponent is watching this first snowball, you throw a second one at a low angle timed to arrive before or at the same time as the first one. Assume both snowballs are thrown with a speed of 34.8 m/s. The first one is thrown at an angle of 70◦ with respect to the horizontal.

At what angle should the second snowball be thrown to arrive at the same point as the first?
Answer in units of degrees

Answer 1

20 degrees

Step-by-step explanation:

Given that,

Speeds of both snowballs is 34.8 m/s

The first one is thrown at an angle of 70◦ with respect to the horizontal. We need to find the angle at which should the second snowball be thrown to arrive at the same point as the first.

We need to find the angle at which the second snowball be thrown to arrive at the same point as the first. We can find the distances of both balls and equate them.

It means, range of both projectiles are equal. So,

`(u^2\sin2\theta_1)/(g)=(u^2\sin2\theta_2)/(g)`

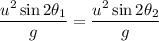
We have,
`\theta_1=70^(\circ)`

So,

`\theta_2=(1)/(2)(\sin^(-1)(\sin2\theta_1))\\\\\theta_2=(1)/(2)(\sin^(-1)(\sin(140))\\\\\theta_2=20^(\circ)`

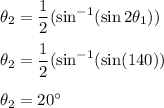
Hence, the second snowball is thrown at an angle of 20 degrees.