Answer:
The x-coordinate of point B that bisects AC is
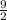 .
.
Explanation:
The statement is not correct, the correct form is:
Jane drew a point A located at (-3,0) and point Clocated at (12,-6). What is the x-coordinate of point B that bisects AC?
Where a point bisects a segment, it means that segment is divided into two equal parts. If we know that
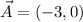 and
and
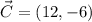 are endpoints of the segment, the location of the endpoint can be found by the following vectorial formula:
are endpoints of the segment, the location of the endpoint can be found by the following vectorial formula:
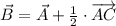
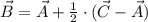
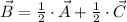
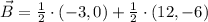

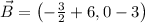
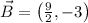
The x-coordinate of point B corresponds to the first component of the ordered pair found above, that is,
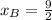 .
.
The x-coordinate of point B that bisects AC is
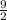 .
.