Answer:
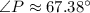
Explanation:
We want to find the measure of ∠P.
To do so, we can use one of the three trigonometric functions.
Since we know the lengths of all of the sides, it doesn't matter which one we use: we will get the same result.
Let's use the sine ratio. Recall that sine is the ratio of the opposite side to the hypotenuse. That is:
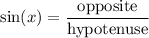
Substitute ∠P for x. So:
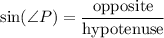
The opposite side to ∠P is 12. The hypotenuse is 13. Hence:
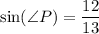
We can take the inverse sine of both sides:
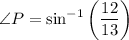
Use a calculator. Make sure you're in degrees mode!
So, the measure of our angle is:
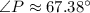
And we're done!