Answer:
Show that if
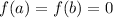 for some
for some
![a,\, b \in [-2,\, 2]](https://img.qammunity.org/2023/formulas/mathematics/high-school/f5xdpi1ll289q5fr2rs3b0l73p4n1hvogr.png) where
where
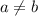 , then by Rolle's Theorem
, then by Rolle's Theorem
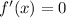 for some
for some
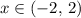 . However, no such
. However, no such
 exists since
exists since
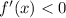 for all
for all
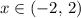 .
.
Note that Rolle's Theorem alone does not give the exact value of the root. Neither does this theorem guarantee that a root exists in this interval.
Explanation:
The function
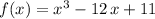 is continuous and differentiable over
is continuous and differentiable over
![[-2,\, 2]](https://img.qammunity.org/2023/formulas/mathematics/high-school/9g8xjnj87jpln3wpsjm0n0dh8k8dba0lnh.png) . By Rolle's Theorem. if
. By Rolle's Theorem. if
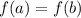 for some
for some
![a,\, b \in [2,\, -2]](https://img.qammunity.org/2023/formulas/mathematics/high-school/lhsf1trlrsj77bz2y8v0pgw6lhu6gkzfss.png) where
where
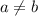 , then there would exist
, then there would exist
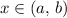 such that
such that
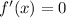 .
.
Assume by contradiction
 does have more than one roots over
does have more than one roots over
![[-2,\, 2]](https://img.qammunity.org/2023/formulas/mathematics/high-school/9g8xjnj87jpln3wpsjm0n0dh8k8dba0lnh.png) . Let
. Let
 and
and
 be (two of the) roots, such that
be (two of the) roots, such that
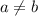 . Notice that
. Notice that
 just as Rolle's Theorem requires. Thus- by Rolle's Theorem- there would exist
just as Rolle's Theorem requires. Thus- by Rolle's Theorem- there would exist
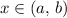 such that
such that
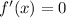 .
.
However, no such
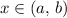 could exist. Notice that
could exist. Notice that
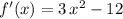 , which is a parabola opening upwards. The only zeros of
, which is a parabola opening upwards. The only zeros of
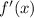 are
are
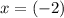 and
and
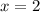 .
.
However, neither
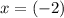 nor
nor
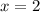 are included in the open interval
are included in the open interval
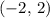 . Additionally,
. Additionally,
![a,\, b \in [-2,\, 2]](https://img.qammunity.org/2023/formulas/mathematics/high-school/f5xdpi1ll289q5fr2rs3b0l73p4n1hvogr.png) , meaning that
, meaning that
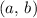 is a subset of the open interval
is a subset of the open interval
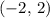 . Thus, neither zero would be in the subset
. Thus, neither zero would be in the subset
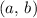 . In other words, there is no
. In other words, there is no
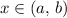 such that
such that
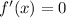 . Contradiction.
. Contradiction.
Hence,
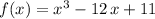 has at most one root over the interval
has at most one root over the interval
![[-2,\, 2]](https://img.qammunity.org/2023/formulas/mathematics/high-school/9g8xjnj87jpln3wpsjm0n0dh8k8dba0lnh.png) .
.