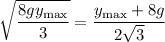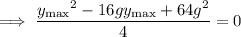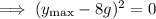Let
 be the initial speed (m/s), so that
be the initial speed (m/s), so that
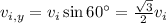 (also m/s) is the vertical component of the initial velocity vector.
(also m/s) is the vertical component of the initial velocity vector.
Recall that
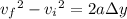
where
 and
and
 are the initial and final velocities,
are the initial and final velocities,
 is the acceleration, and
is the acceleration, and
 is the vertical displacement. At its maximum height (which the question seems to say occurs after 4 seconds), the velocity is 0, and throughout its motion the projectile is under the influence of gravity so that
is the vertical displacement. At its maximum height (which the question seems to say occurs after 4 seconds), the velocity is 0, and throughout its motion the projectile is under the influence of gravity so that
 and g = 9.80.
and g = 9.80.
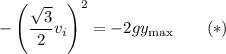
The projectile's height
 (m) at time
(m) at time
 (s) is
(s) is
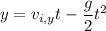
so that when t = 4 s, its height is
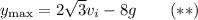
Solve
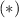 and
and
 for
for
 , then solve for
, then solve for
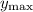 :
:
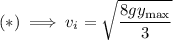
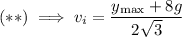
Then