Answer:
The equation of the parabola is
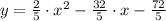 . The average rate of change of the parabola is -4.
. The average rate of change of the parabola is -4.
Explanation:
We must remember that a parabola is represented by a quadratic function, which can be formed by knowing three different points. A quadratic function is standard form is represented by:

Where:
 - Independent variable, dimensionless.
- Independent variable, dimensionless.
 - Dependent variable, dimensionless.
- Dependent variable, dimensionless.
 ,
,
 ,
,
 - Coefficients, dimensionless.
- Coefficients, dimensionless.
If we know that
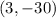 ,
,
 and
and
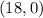 are part of the parabola, the following linear system of equations is formed:
are part of the parabola, the following linear system of equations is formed:
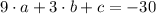
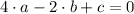
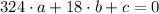
This system can be solved both by algebraic means (substitution, elimination, equalization, determinant) and by numerical methods. The solution of the linear system is:
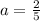 ,
,
 ,
,
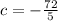 .
.
The equation of the parabola is
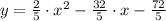 .
.
Now, we calculate the average rate of change (
 ), dimensionless, between
), dimensionless, between
 and
and
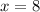 by using the formula of secant line slope:
by using the formula of secant line slope:
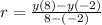
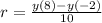

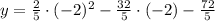
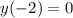
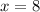

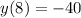
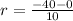
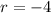
The average rate of change of the parabola is -4.