If one kilogram equals 2.2 pounds how many kilograms equal 112 pounds

Question

asked Apr 3, 2021 7.2k views

2 Answers

Cengizkrbck · Answer 1 · 2021-04-06T05:28:19+0000

Answer & Step-by-step explanation:

Assuming that there is a constant rate of change, we can use the equation:

y=kx

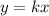
k is the constant rate of change. Set up an equation in which the pounds are determined by the rate of change between kilograms and pounds:

1=k(2.2)

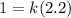
Isolate the variable k:

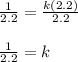
$(1)/(2.2)=(k(2.2))/(2.2)\\\\(1)/(2.2)=k$

Set up another equation like so:

(y)/(x)=(y)/(x)

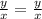
Insert values:

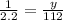
(1)/(2.2)=(y)/(112)

Solve for y. Cross multiply:

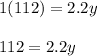
$1(112)=2.2y\\\\112=2.2y$

Isolate the variable. Divide both sides by 2.2:

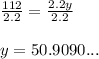
$(112)/(2.2)=(2.2y)/(2.2) \\\\ y=50.9090...$

So, there are about 50.9 kilograms in 112 pounds.

:Done